Cette page vous présente toutes les réalisations effectuées dans la cadre de la collaboration avec le LEO pour la préparation de différents supports à des fins pédagogique et de recherche.
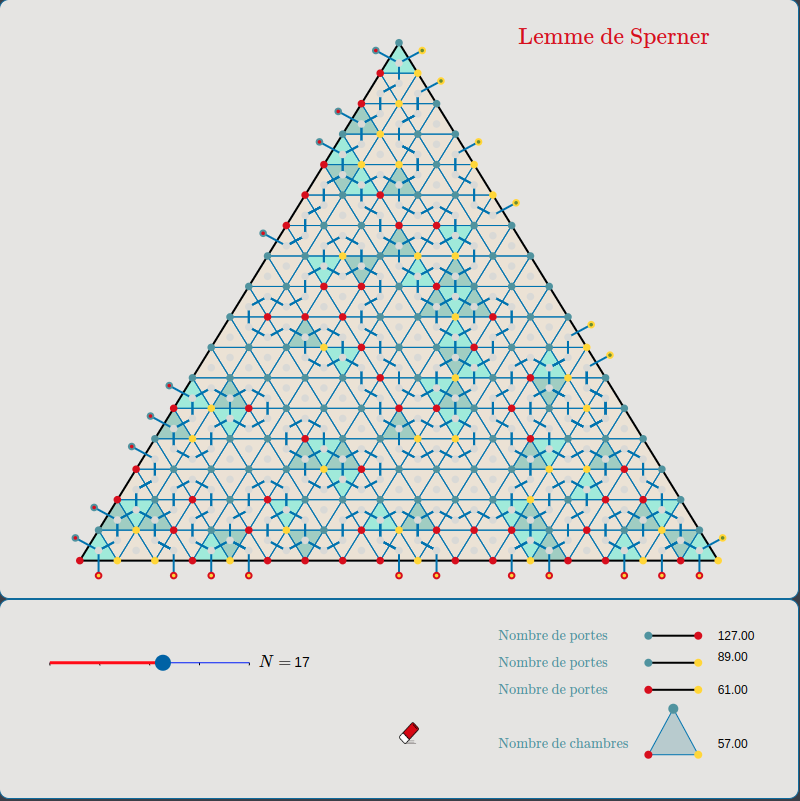
Lemme de Sperner (1928) : Considérons un triangle dont les sommets se distinguent par 3 couleurs. Les côtés sont divisés de telle sorte à reproduire le graphique de droite (en dimension 2). Les intersections sont colorées au hasard sur les deux couleurs qui marquent les sommets qui déterminent les côtés et sur les trois couleurs pour les points intérieur. Alors, il existe au moins un triangle intérieur dont les sommets possèdent les 3 couleurs.
Ce théorème est équivalent au Théorème du Point Fixe de Brouwer (1912). En économie, Il permet de démontrer, entre autres, l’existence de l’Équilibre Général (1954) (Théorème d’Arrow-Debreu) ou de l’Équilibre de Nash (1951) .
Ici, le lemme de Sperner est présenté en dimension 2, mais il est valable pour toute dimension ⩾ 1. ici on choisit un côté. On appelle porte, un segment dont les deux extrémités sont de couleur différente. On rentre dans le triangle par une porte et on évolue par ce type de porte jusqu’à ce que, soit on ressorte, soit qu’on aboutisse sur un triangle à trois couleurs. Comme ressortir consomme deux portes et que le nombre de porte est nécessairement impair, il existe au moins un triangle tricolor dans l’intérieur de grand triangle.

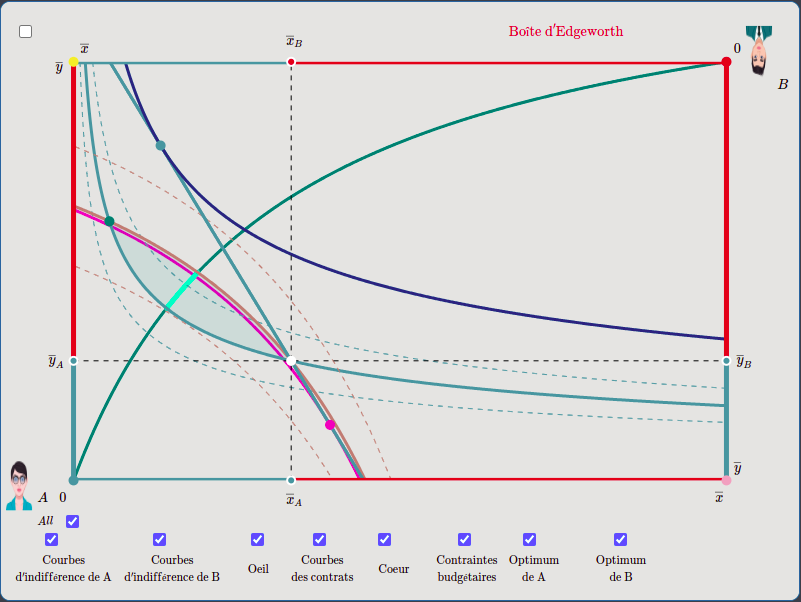
Boîte d’Edgeworth : La boîte d’Edgeworth (qui n’a pas été conçue par Francis Isidro Edgeworth lui-même mais par Vilfredo Pareto et Arthur Bowley) permet de décrire à la fois l’Optimum de Pareto et l‘Équilibre général d’une Économie d’Échange. Elle illustre parfaitement, dans le cas de deux agents (ou de deux catégories d’agents identiques), le fait que le système de prix d’équilibre d’une économie d’échange est aussi un Optimum de Pareto, si un certain nombre de conditions génériques est vérifié.

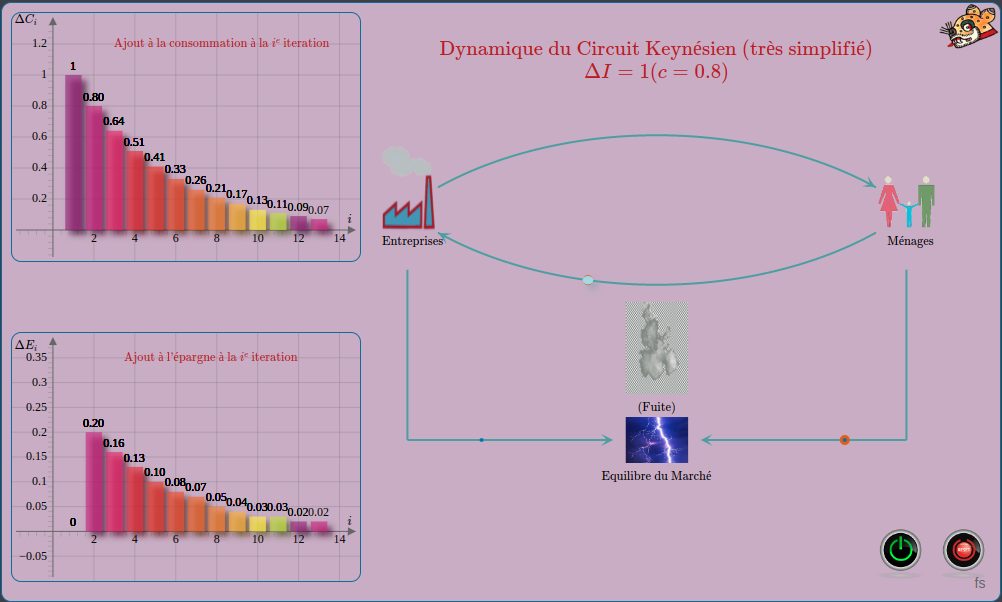
Circuit Keynésien (simplifié) : Cette présentation explique dynamiquement, étape par étape, ce qui se produit dans un circuit économique simplifié par la présence de deux types d’agents (les ménages et les entreprises) quand les entreprises décident d’accroître l’investissement. Elle traduit l’enchaînement des accroissements des consommations qui se retransforment en revenu pour les ménages. Mais; du fait de la fuite que représente l’épargne hors du système, ces accroissements sont de plus en plus réduits.

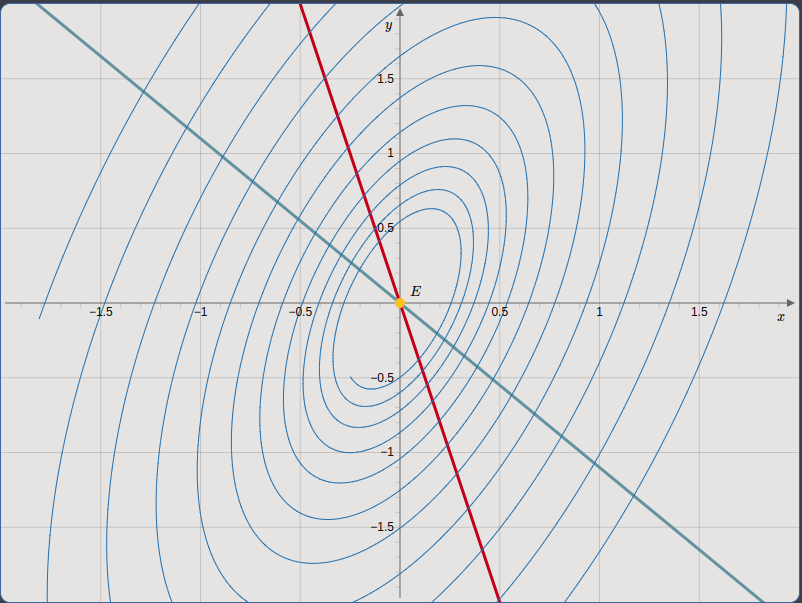
Système d’équations différentielles linéaires : cette petite application permet de simuler l’évolution d’un système d’équations différentielles linéaires et de tracer le champ de force qui lui est associé.
Une fois les paramètres entrés dans l’application, elle demande à SageCell de trouver la solution, puis elle la trace dans JsxGraph. On peut cliquer sur un point du plan pour changer le point de départ.


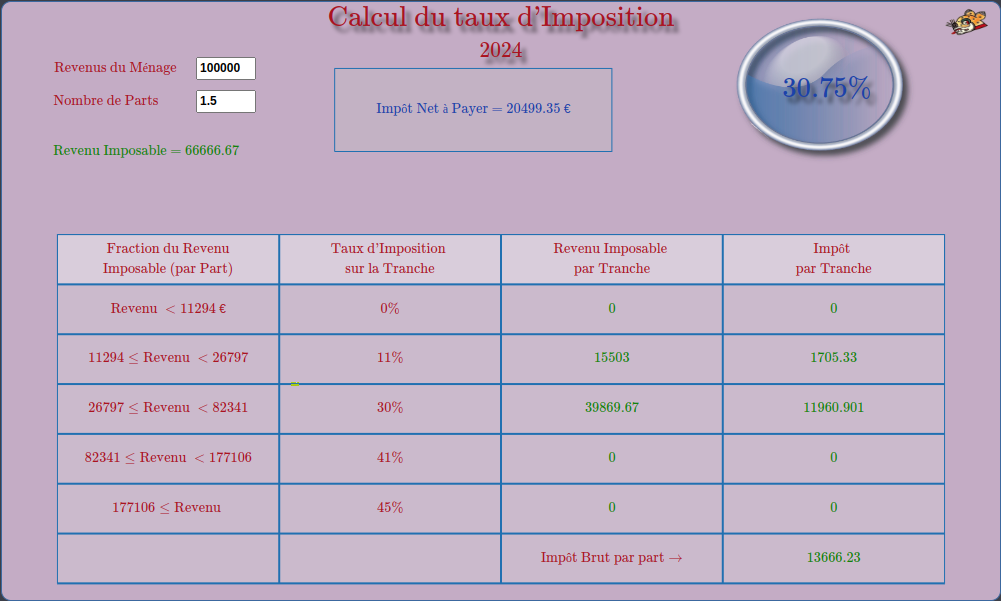
Calcul d’impôt : cette feuille de calcul évalue l’impôt sur le revenu qu’un ménage doit payer en fonction de son revenu et du nombre de parts qui le caractérise.
Ainsi, elle retourne la pression fiscale marginale auquel est soumis ce ménage.
Elle permet de comprendre la décomposition du revenu imposable par tranche de taxation (en 2024).

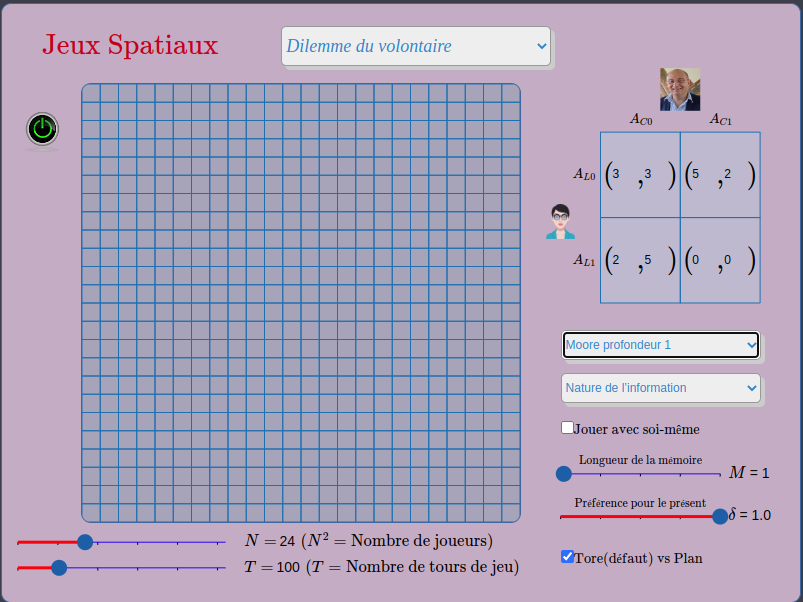
Jeux spatiaux : les jeux spatiaux sont un cas particulier de la Théorie des Jeux. Chaque joueur joue un certain nombre de fois (adaptable) avec ses voisins (il existe plusieurs types de voisinages). Au commencement, tous les joueurs adoptent la même stratégie parmi les deux disponibles. S’il découvre que l’un de ses voisins réalise un meilleur score que lui, il change de stratégie comme dans l’article de Nowak et May (1992).